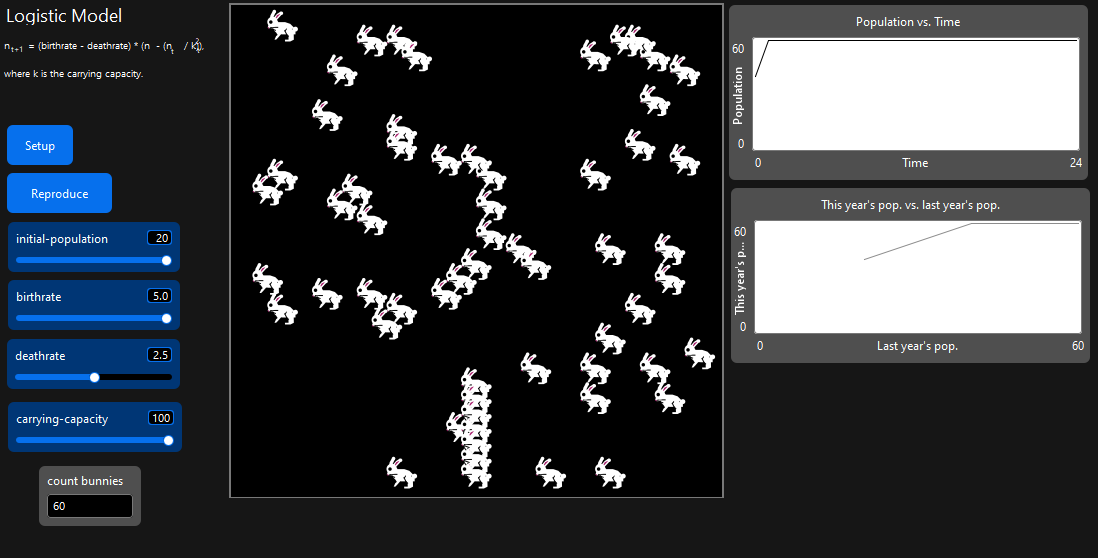
Have you ever wondered how complex behaviors in nature, like population growth, can emerge from surprisingly simple rules? Enter the Logistic Map, a mathematical model that’s a cornerstone in the study of chaos theory and complex systems.
It’s defined by the recursive equation:
![]()
Here, ![]() is the growth rate, and
is the growth rate, and ![]() represents the population (or system state) at a given time
represents the population (or system state) at a given time ![]() . The magic of this simple equation is how it can produce a stable, predictable outcome with one set of
. The magic of this simple equation is how it can produce a stable, predictable outcome with one set of ![]() values, and complete chaos with others!
values, and complete chaos with others!
What is a Fixed Point?
In the context of the logistic map, a fixed point is a value that, once reached, remains constant in all subsequent iterations. It’s a point of stability where the system settles. Mathematically, a fixed point, ![]() , satisfies the condition:
, satisfies the condition:
![]()
This means the value ![]() at time
at time ![]() results in the exact same value at time
results in the exact same value at time ![]() .
.
Finding the Fixed Point: Step-by-Step
The quiz example provides a perfect scenario to demonstrate how a system finds its stability.
The Task:
We are given ![]() and an initial value
and an initial value ![]() . We need to find the fixed point.
. We need to find the fixed point.
Method 1: Iterative Calculation (The Simulation Approach)
We’ll start with ![]() and calculate
and calculate ![]() until the value stops changing significantly.
until the value stops changing significantly.
| Iteration ( |
Calculation: |
Result ( |
|---|---|---|
| t=0 | ||
| t=1 | ||
| t=2 |
Since ![]() and
and ![]() are the same, the system has converged! The fixed point is 0.6.
are the same, the system has converged! The fixed point is 0.6.
The visual from the NetLogo simulation (which models a similar logistic system) confirms this behavior: the population quickly rises from its initial state to a stable maximum.
Method 2: Analytical Calculation (The Fixed Point Formula)
To be absolutely sure, we can use the fixed point formula ![]() and solve for
and solve for ![]() using
using ![]() .
.
- Set the equation:
![Rendered by QuickLaTeX.com \[x^* = 2.5 (x^* - {x^*}^2)\]](https://jeyhun.net/wp-content/ql-cache/quicklatex.com-6ce1ddc045163d93bd6c4a24f0c903d0_l3.png)
- Divide both sides by
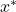 (assuming
(assuming 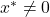 ):
):
![Rendered by QuickLaTeX.com \[1 = 2.5 (1 - x^*)\]](https://jeyhun.net/wp-content/ql-cache/quicklatex.com-ac5710be850e39f3c712a6c5818cfacf_l3.png)
- Divide by
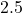 (or multiply by
(or multiply by 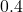 ):
):
![Rendered by QuickLaTeX.com \[\frac{1}{2.5} = 1 - x^*\]](https://jeyhun.net/wp-content/ql-cache/quicklatex.com-ea325f315a2800af0eee5b4827aa2ded_l3.png)
![Rendered by QuickLaTeX.com \[0.4 = 1 - x^*\]](https://jeyhun.net/wp-content/ql-cache/quicklatex.com-e751262f2f5963652699ad175d708455_l3.png)
- Solve for
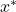 (rearrange):
(rearrange):
![Rendered by QuickLaTeX.com \[x^* = 1 - 0.4\]](https://jeyhun.net/wp-content/ql-cache/quicklatex.com-db967099600be34ecffd39d5cbbaa37a_l3.png)
![Rendered by QuickLaTeX.com \[\mathbf{x^* = 0.6}\]](https://jeyhun.net/wp-content/ql-cache/quicklatex.com-54e27a78150107389fb24f186b41f6ad_l3.png)
Both methods confirm that the system stabilizes at 0.6.
Conclusion
This simple problem beautifully illustrates how a deterministic equation—the Logistic Map—can lead to a stable, predictable outcome, a fixed point. For ![]() and
and ![]() , the system quickly approaches and settles at 0.6 (Option b in the quiz).
, the system quickly approaches and settles at 0.6 (Option b in the quiz).
The Logistic Map is a foundational tool in understanding how complex behaviors emerge from simple rules. If you increase the ![]() value, you start to see fascinating phenomena like period-doubling and eventually, chaos!
value, you start to see fascinating phenomena like period-doubling and eventually, chaos!