The Koch curve is one of the earliest and most famous examples of a fractal—a shape that displays self-similarity, meaning it looks similar at any level of magnification. It was first described by Swedish mathematician Helge von Koch in 1904 as a curve that is continuous but nowhere differentiable.

How the Koch Curve Is Constructed

The Koch curve begins with a simple straight line segment. The process of creating the curve involves an iterative procedure:

1. Divide the line segment into three equal parts.
2. Construct an equilateral triangle on the middle segment.
3. Remove the base of that triangle.

Each iteration adds more detail to the curve, and the total length of the curve increases with every step.

Mathematical Calculation

If the initial length of the line is , then at each iteration:

• The line is divided into 4 new segments (each of length ).
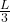• The total length after the first iteration becomes .

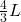In general, after iterations, the total length of the curve is:

As approaches infinity, the length of the curve tends to infinity, even though it is contained within a finite area. This paradoxical property is what makes the Koch curve so fascinating.

Fractal Dimension

The Koch curve also demonstrates the concept of fractal dimension. Its dimension can be calculated using the formula:

This means the Koch curve has a dimension between 1 (a line) and 2 (a plane), indicating it is more complex than a simple line but does not fill a two-dimensional area.

Examples in Nature

The Koch curve is not just a mathematical curiosity—it models real patterns found in nature. Many natural forms display fractal-like self-similarity similar to the Koch curve:

• Snowflakes: The intricate edges of snowflakes closely resemble the recursive pattern of the Koch curve.
• Coastlines: The jagged edges of coastlines can be described using fractal geometry similar to the Koch curve, where more detail appears at smaller scales.
• Ice crystals and frost patterns: Their branching, repeating structures mirror the same geometric principle.

Why It Is Important

The Koch curve illustrates the power of fractals in describing complex shapes that traditional Euclidean geometry cannot easily represent. Understanding fractals has applications in:

• Computer graphics: Generating natural-looking terrain, mountains, or snowflakes.
• Physics: Modeling irregular surfaces and diffusion phenomena.
• Biology: Studying branching patterns in blood vessels, lungs, and plants.
• Geography: Measuring irregular coastlines and mountain ranges.

Conclusion

The Koch curve serves as a bridge between art, mathematics, and nature. Its infinite complexity emerging from a simple rule demonstrates how fractal geometry helps us understand the hidden order within natural irregularities.

“The simplest rules can create the most complex beauty.” — Inspired by Helge von Koch